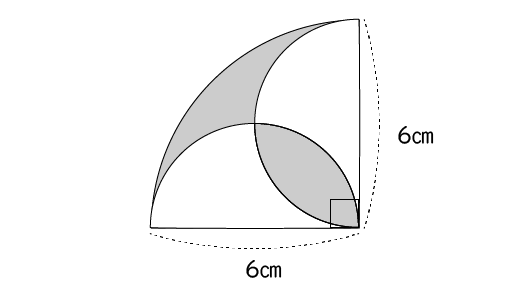
扇形の面積=5×5×314×90°÷360°=(cm 2) 続いて三角形の面積を求めていきます。上で見たように,∠FDBは直角です。このことから三角形の底辺は5cmであり,高さも5cmであることが分かります。よって三角形の面積は次のようになります。 三角形の面積=5×
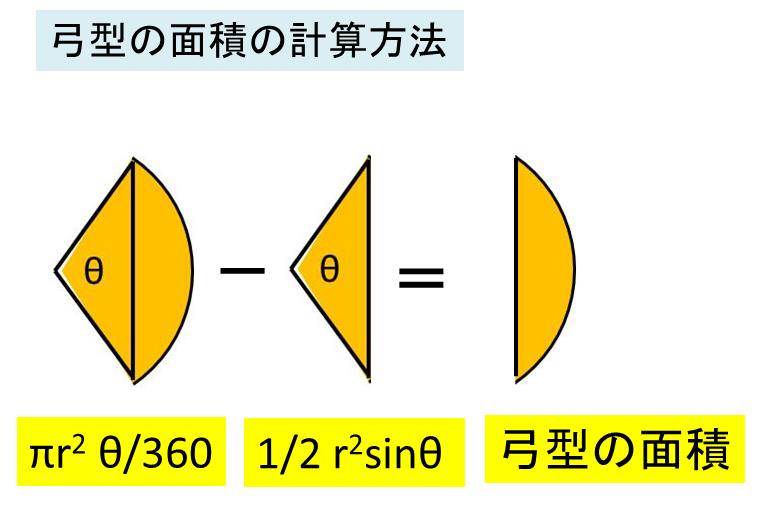
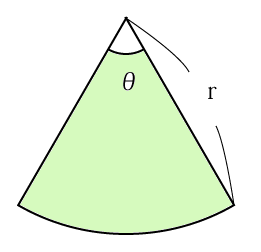
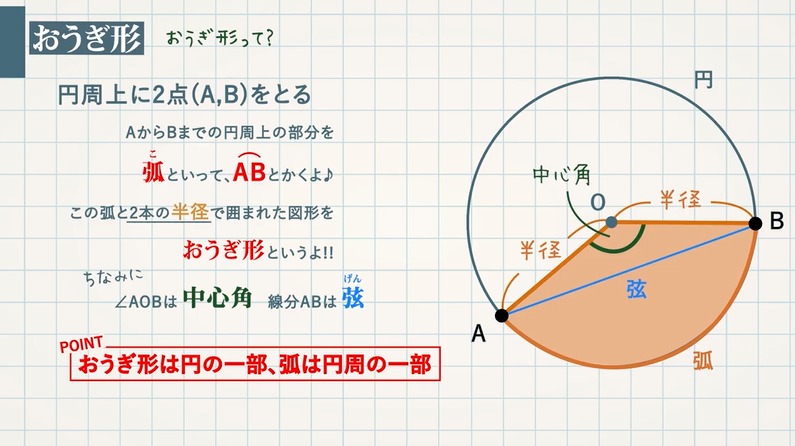
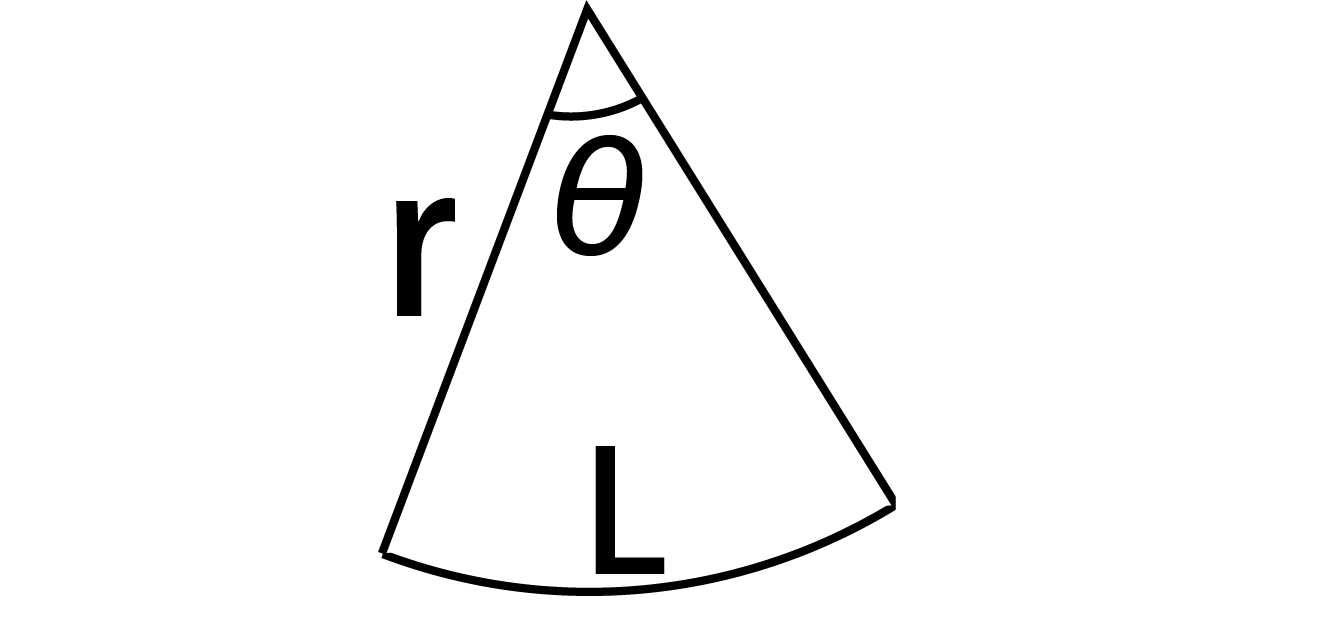
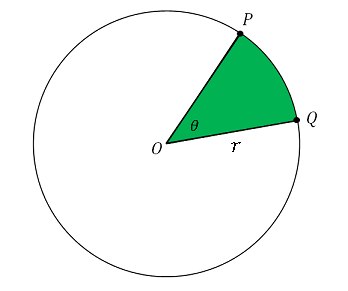
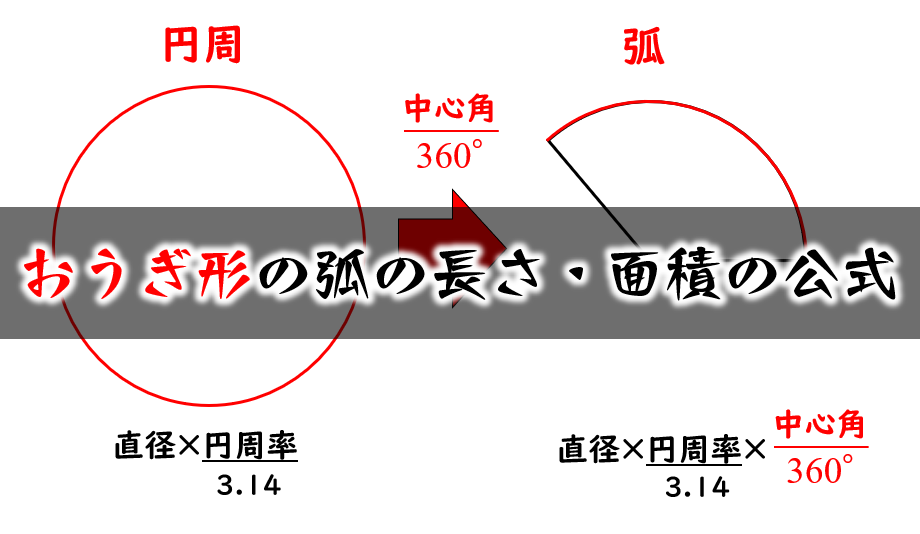
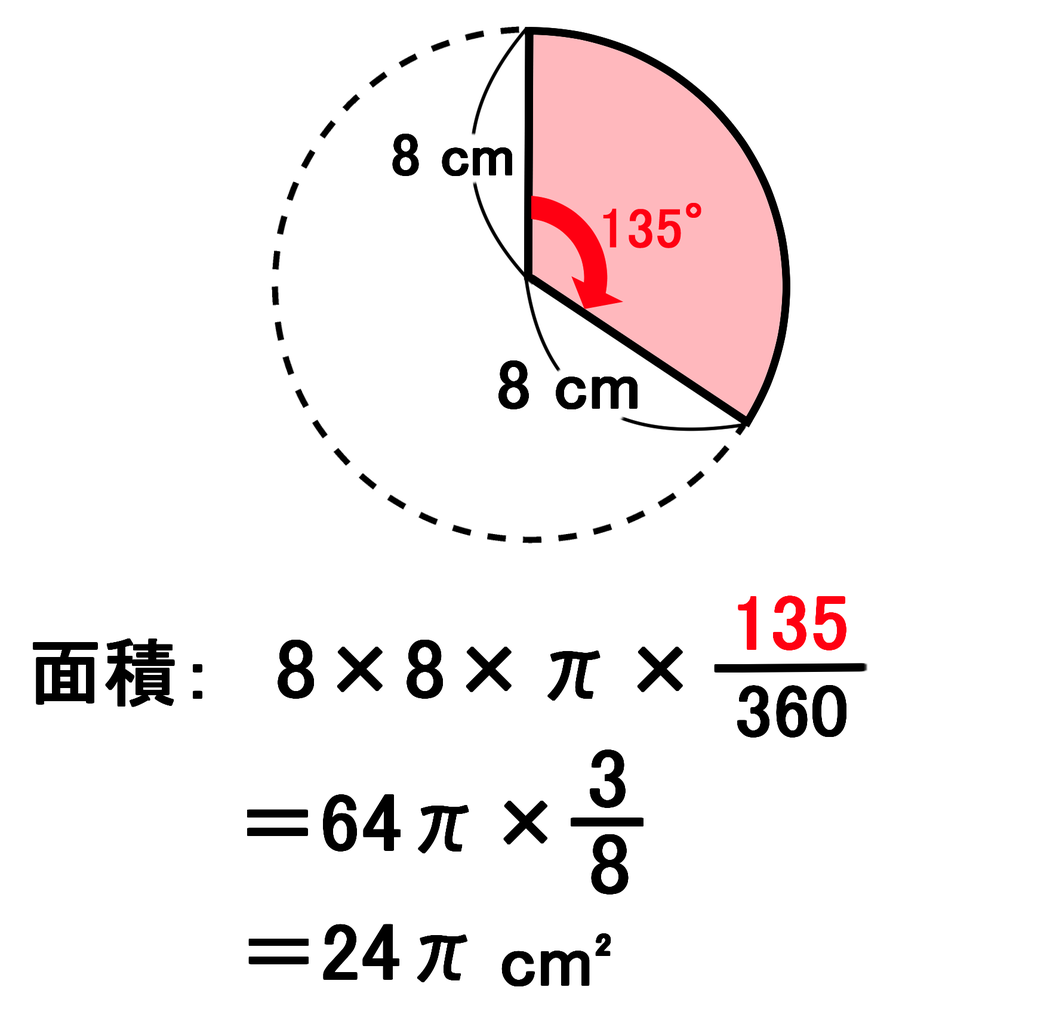
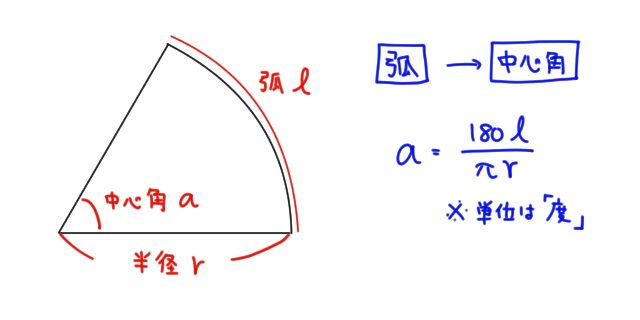
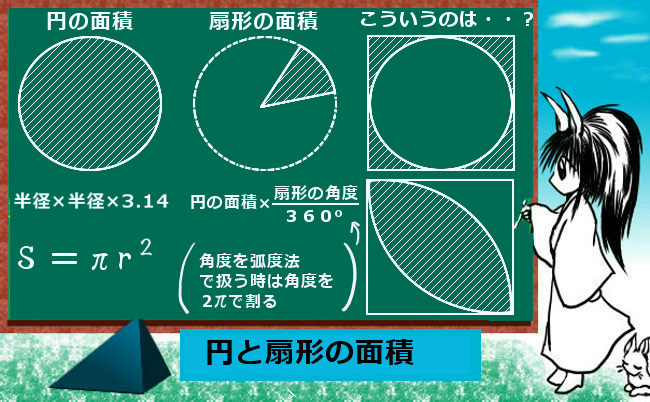
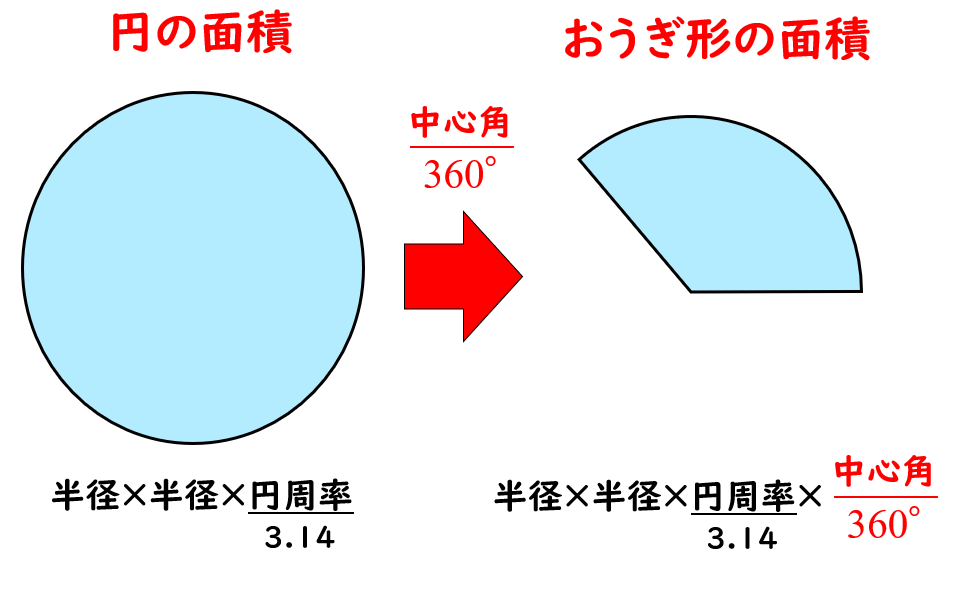
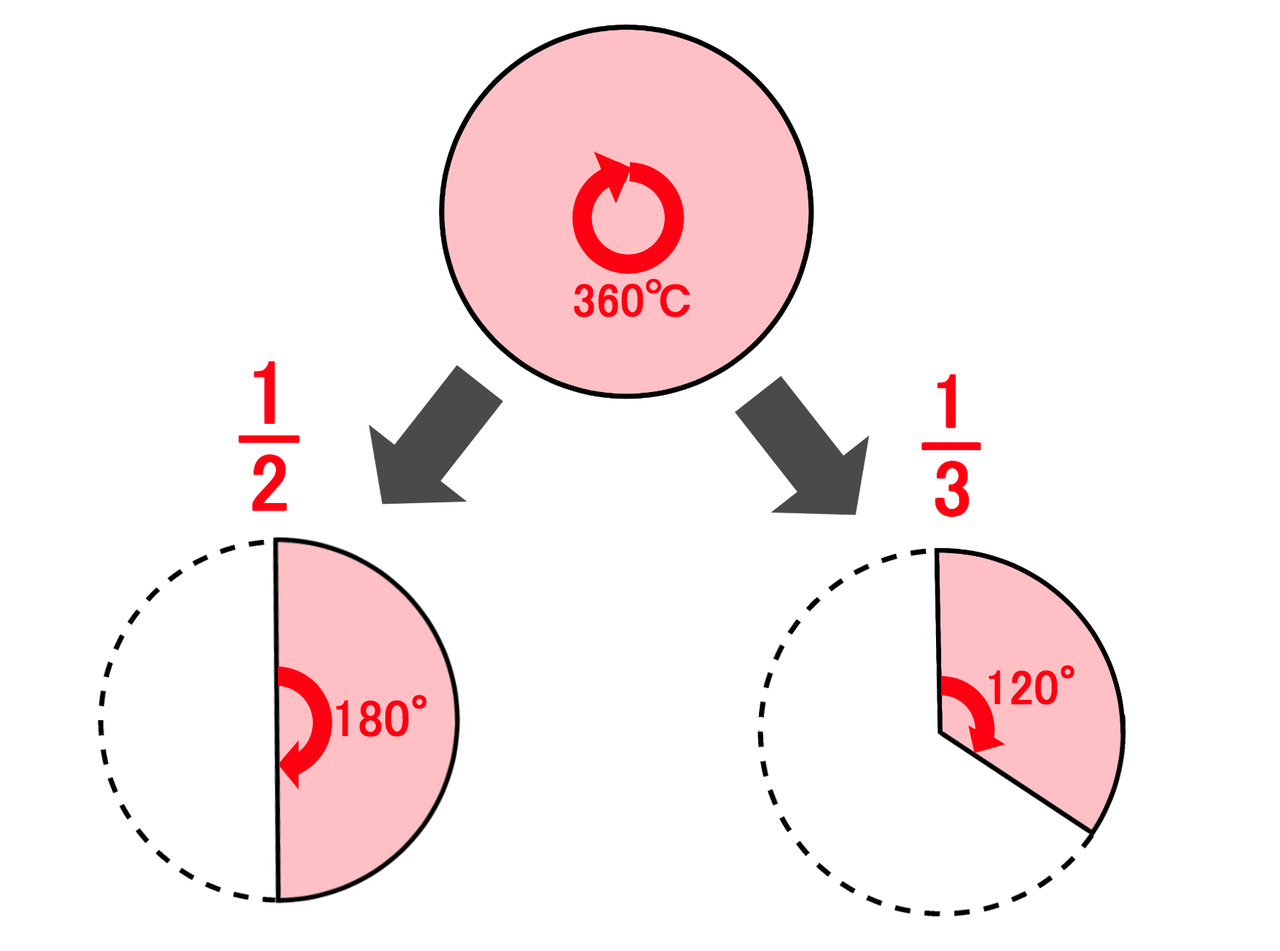
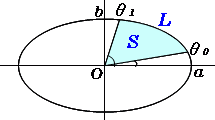
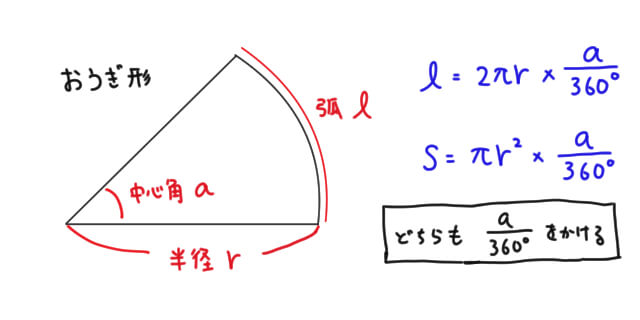
扇形 面積 求め方 角度なし- つまり、円は360度なので、扇形の中心の角度がわかれば以下のような公式に当てはめるだけで問題を解くことができます。 おうぎ形の弧の長さ = 直径 × 円周率 × 中心角 ÷ 360 $$扇形の弧の長さ=直径 \times 円周率\times \frac{中心角}{360}$$ 円の面積 扇型に面積 S S = 1 2 r 2 θ まずはこれらを自分の手で計算して出してみましょう。 大事です。 さてここからもう一つ公式を作ってみましょう。 難しくありません。 1 つ目の式を 2 つ目に代入するだけです。 1 つ目の式から θ = l r とできますので、弧度法の角度 θ を消せば S = 1 2 r 2 θ = 1 2 r 2 × l r = 1 2 r l となります。 もし 半径と弧の長さがわかっているのであれば 、その情報だけで 扇
扇形 面積 求め方 角度なしのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「扇形 面積 求め方 角度なし」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「扇形 面積 求め方 角度なし」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「扇形 面積 求め方 角度なし」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「扇形 面積 求め方 角度なし」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「扇形 面積 求め方 角度なし」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「扇形 面積 求め方 角度なし」の画像ギャラリー、詳細は各画像をクリックしてください。
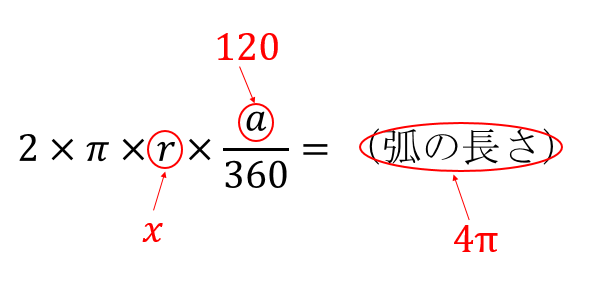 |  |  |
 |  |  |
 |  |  |
 |  | |
「扇形 面積 求め方 角度なし」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「扇形 面積 求め方 角度なし」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
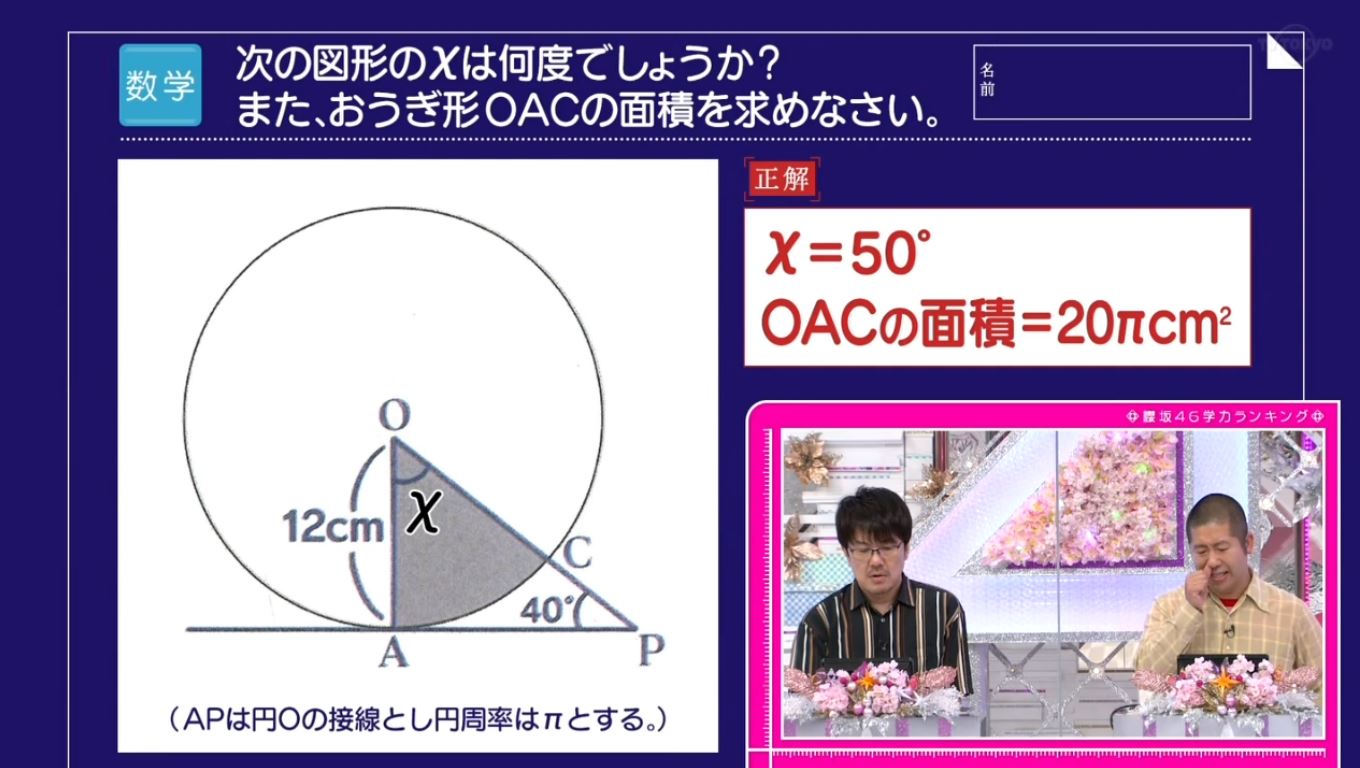
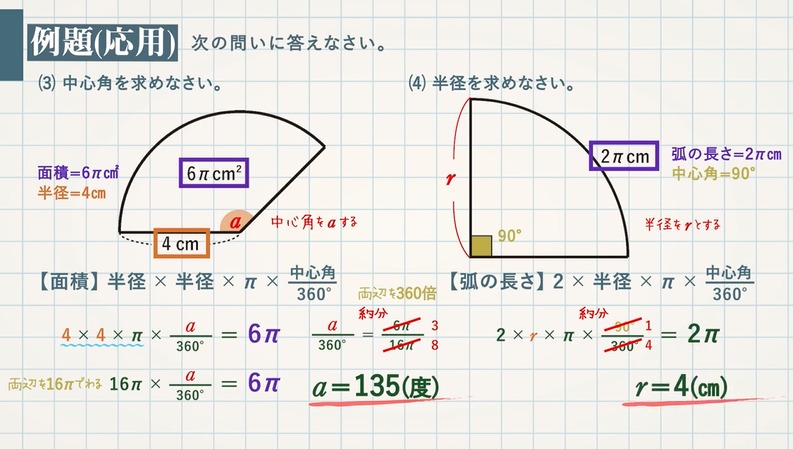
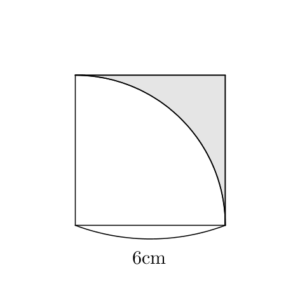
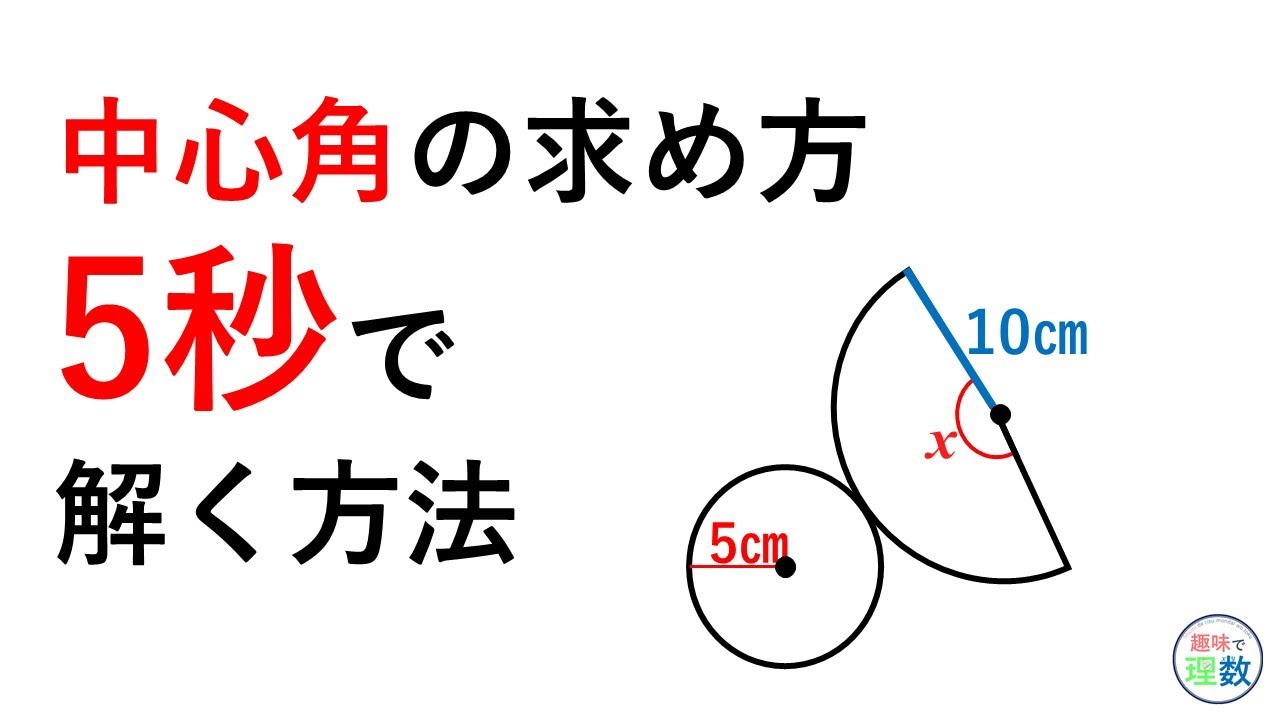
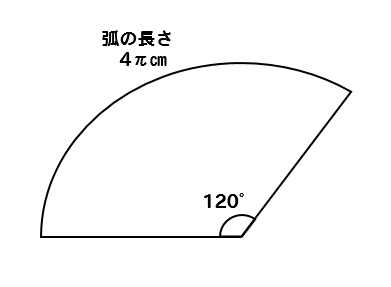
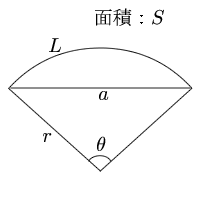
扇形の面積と弧の長さがわかっているときの、扇形の角度の求め方を教えてください。 〔回答〕 以下の説明において、 S=おうぎ形の面積,ℓ=弧の長さ,r=おうぎ形の半径,x=中心角の大きさ とします。 まず、おうぎ形の面積に関しては (1 扇形の面積の求め方を教えて下さい!m(_ _)m 現役学生ではないので全く分からずです(泣)試験は明日なのに(ToT)情けない(泣)問題は半径は6で、弧の長さは4πである扇形の面積を求めよ。 です。 どうぞ宜しくお願い致します。m(_ _)m直径
Incoming Term: 扇形 面積 求め方 角度なし,



